THERMOMÈTRES GÉOLOGIQUES

THERMOMÈTRES GÉOLOGIQUES

Dans l’étude des phénomènes géologiques, la détermination de la température régnant au cours des différents processus qui ont donné et donnent naissance aux matériaux terrestres est un élément très important. Parmi ces phénomènes, il en est qui sont actuels et accessibles. Le problème de la mesure de la température est alors seulement un problème technique, parfois délicat, comme la mesure de la température de solidification d’une lave, mais généralement soluble.

Plus complexe est la détermination des températures qui ont régné au cours d’événements passés (ayant souvent leur équivalent présent mais inaccessible), c’est-à-dire de ce qu’on peut appeler des paléotempératures .

À cet égard, tous les matériaux terrestres se comportent comme des boîtes ayant enfermé un certain nombre d’informations sur les conditions de leur genèse, par exemple des horloges susceptibles de donner leur âge, des indicateurs de déformation qui donnent une idée des contraintes auxquelles ils ont été soumis. Ainsi en est-il de la température; mais, comme dans le cas des autres paramètres, il convient de savoir à quelle étape de la formation du matériau la «boîte» s’est fermée et si elle ne s’est pas rouverte depuis lors. On conçoit aisément que cela pose des problèmes souvent assez ardus.

Parmi les méthodes thermométriques dont on dispose, un petit nombre exploite des données cinétiques (par exemple, disparition des traces de fission dans les minéraux, «guérison» des états métamictes, thermoluminescence), mais la plupart sont fondées sur l’étude des équilibres existant dans les matériaux utilisés. Par conséquent, le postulat fondamental est que de tels équilibres ont effectivement existé au moment de leur formation. Les équilibres en question peuvent être des équilibres biologiques. C’est ainsi que des associations de faunes ou de flores permettent de fixer, dans les terrains sédimentaires, les limites du domaine des températures existant à l’époque de la sédimentation. Par exemple, l’existence de formations coralliennes est l’indice de températures moyennes de 25 à 30 ⁰C. De tels indicateurs sont largement utilisés en paléoclimatologie et en paléogéographie (cf. PALÉOCLIMATOLOGIE, PALÉOGÉOGRAPHIE). Néanmoins, ils fixent seulement un domaine de variations, et non un relevé exact. En outre, ils ne concernent qu’une frange assez restreinte parmi tous les phénomènes étudiés en géologie. C’est pourquoi on se limitera ici à l’exposé des méthodes physico-chimiques, c’est-à-dire les méthodes «cinétiques» déjà citées, l’utilisation des inclusions fluides dans les cristaux et, surtout, l’étude des équilibres thermodynamiques.

La notion de paléotempérature

Quand on considère une roche, son histoire correspond généralement à une série continue de températures, de laquelle n’importe quelle méthode ne permettra d’extraire qu’une seule donnée, car les thermomètres géologiques ne sont ordinairement pas des thermomètres «enregistreurs». Le problème est de savoir à quelle partie de l’histoire de la roche appartient cette donnée, et la réponse peut être différente suivant la méthode utilisée. Ainsi on obtient la température dite de formation, température à laquelle se sont individualisés les principaux minéraux présents dans la roche qui constituent la paragenèse caractéristique. Le plus souvent, d’ailleurs, cette individualisation correspond non pas à une température mais à un intervalle de températures plus ou moins grand. Puis, à cette paragenèse principale peuvent s’ajouter ou se substituer par la suite un certain nombre de minéraux secondaires en plus ou moins grande quantité, des défauts peuvent apparaître ou disparaître dans les minéraux, tout cela au cours d’une histoire thermique plus ou moins compliquée. Pour pouvoir déterminer alors une «température de formation», il faut disposer d’un état d’équilibre thermodynamique existant au moment de cette formation. Même en laissant de côté les cas où cet équilibre n’était pas en fait réalisé, il faut, pour pouvoir exploiter les données, que cet équilibre ait été «figé» assez rapidement pour nous parvenir intact. On peut donc, de ce point de vue, diviser les phénomènes géologiques en trois catégories:

– Les phénomènes de basse température ou de surface . Pour les matériaux formés au cours de ces phénomènes, on définit souvent avec précision une température de formation (par exemple, formation de calcite ou de silice par précipitation). Les équilibres thermodynamiques existant au moment de la formation seront généralement figés jusqu’à l’époque actuelle, pourvu que leur histoire thermique postérieure ne comporte pas d’épisodes à température supérieure à 100 ⁰C. C’est le cas de beaucoup de matériaux sédimentaires pour lesquels on peut, par conséquent, espérer obtenir une température de formation.

– Les phénomèmes de haute température suivis d’un refroidissement brutal , c’est-à-dire typiquement les phénomènes volcaniques. Dans ce cas, les équilibres existant à haute température seront, eux aussi, en général figés car la vitesse de refroidissement ne permettra pas de réarrangement postérieur des édifices atomiques. L’étude des équilibres existants peut permettre alors de déterminer la température de solidification de la lave.

– Les phénomènes de moyenne et de haute température à refroidissement plus ou moins rapide . Dans ce cas, la mobilité des atomes peut rester très importante pendant une grande partie du refroidissement, et les édifices formés à haute température peuvent se détruire pour donner d’autres édifices, plus stables à mesure que la température décroît. Les édifices que nous observons actuellement, c’est-à-dire les associations minérales, correspondent, dans ce cas, à la température à partir de laquelle la mobilité des atomes est devenue trop faible pour modifier dans un laps de temps suffisamment bref la configuration de l’ensemble. C’est ainsi qu’on observera très souvent dans un granite un mélange de feldspath potassique (orthose) et de feldspath sodique (albite), alors qu’au moment de la cristallisation de la roche ces minéraux ne formaient qu’une seule phase. Il est possible de retrouver la trace de cette phase préexistante dans la texture de la roche (structure perthitique d’exsolution), mais la notion de température de formation de l’assemblage total n’a dans ce cas aucun sens. Ce sera le cas à peu près général de toutes les roches plutoniques, c’est-à-dire des roches qui se sont formées par refroidissement lent d’un magma dans un réservoir magmatique (gabbros, granites, etc.). Pour ces roches, la cristallisation a pu s’effectuer dans un intervalle de températures notable et il a pu se produire des réarrangements importants après la cristallisation. Ce peut être le cas également pour des roches métamorphiques.

En dehors de la température de formation, il peut exister dans la roche des indications sur des réchauffements subis par elle après sa formation. Il s’agit souvent de phénomènes majeurs qui modifient complètement la première paragenèse minérale. Dans ces conditions, qui sont typiquement celles du métamorphisme, la plupart des renseignements concernant la formation de la première paragenèse sont perdus, et l’on mesure en fait une deuxième température de formation. Dans quelques cas, néanmoins, la paragenèse primaire n’est que peu (phénomènes de rétromorphose partielle) ou pas modifiée. Dans ce cas, l’examen de certains caractères mineurs des minéraux (défauts, par exemple) permet parfois d’obtenir des indications sur la température du réchauffement. C’est, par exemple, le cas de ce qu’on peut appeler les méthodes cinétiques.

Méthodes cinétiques

Nous ne dirons que peu de chose des méthodes cinétiques, car, bien que l’idée de départ en soit souvent séduisante, elles se heurtent dans la plupart des cas à des difficultés quasi insurmontables. Ce sont, en fait, des méthodes qui permettraient de déterminer la température d’un phénomène si l’on connaît sa durée, et inversement. Elles ne peuvent donc être utilisées en thermométrie si l’on ne possède pas aussi un chronomètre indépendant. Le point de départ est généralement l’existence de défauts dans les cristaux (niveaux d’impuretés, traces de fission dues aux éléments radioactifs, etc.). Sous l’influence d’un réchauffement, ces défauts disparaissent à une vitesse qui dépend de la température suivant une loi du type v = A e ^-E/RT, où E est l’énergie d’activation. Si l’on connaît la durée du réchauffement, le taux initial de défauts, et si l’on suppose que la température est restée constante tout au long du réchauffement, on peut obtenir cette température. On voit que le nombre de conditions à remplir est assez restrictif. En fait, ces méthodes ne peuvent donner de résultats valables que si la température monte assez brutalement à une valeur assez importante par rapport à l’énergie d’activation, c’est-à-dire si la cinétique est rapide. C’est le cas, par exemple, du réchauffement, par une intrusion, de la roche encaissante. En étudiant la disparition des traces de fission dans les cristaux de sphène et d’apatite du granite de Cathedral Peak (Californie) au voisinage d’une intrusion basaltique, L. C. Calk et C. W. Naeser ont ainsi retracé la distribution des températures maximales atteintes autour de cette intrusion: de 650 ⁰C au voisinage de l’intrusion (2 mètres) à 150 ⁰C à 300 mètres.

Étude des inclusions fluides

Cette méthode utilise les fluides emprisonnés dans des cavités par les cristaux au cours de leur formation. Ces fluides ne représentent pas un équilibre de haute température figé. Cependant, on suppose généralement qu’ils ont évolué en système clos depuis leur emprisonnement, c’est-à-dire qu’il n’y a eu ni fuite, ni apport de l’extérieur, ni réaction avec le cristal hôte.

Dans ces conditions, et pourvu que le fluide emprisonné ait une composition suffisamment voisine d’un corps pur, la détermination de sa densité donne des indications sur la pression et la température de remplissage de l’inclusion. En effet, à densité constante (ou encore, si l’on préfère, à volume d’inclusion constant, ce qui est sensiblement vérifié si le solide est suffisamment peu compressible et dilatable), le point figuratif du fluide décrit une courbe dans le plan P-T (isochore). Il suffit de déterminer un point de cette isochore pour l’identifier. On le fait généralement avec assez de précision en déterminant la température de l’équilibre biphasé (liquide-vapeur généralement), ce qui donne le point de l’isochore situé sur la courbe d’équilibre liquide-vapeur du corps pur considéré (H²O ou bien C² dans la plupart des cas). On voit, par exemple, sur la figure 1 le réseau des isochores du gaz carbonique.

Cette méthode est élégante et ne nécessite qu’un matériel relativement réduit (microscope équipé d’une platine chauffante et réfrigérante, pour observer l’apparition de l’équilibre biphasé). Les complications sont de deux ordres:

– Généralement, le fluide contenu dans l’inclusion n’est pas un corps pur. Néanmoins, cette condition est souvent suffisamment près d’être réalisée pour ne pas poser de problèmes trop sérieux. De la même manière, les corrections de dilatation thermique et de compressibilité à appliquer au cristal hôte ne soulèvent pas de difficultés.

– Ici, la difficulté est plus fondamentale: l’isochore ne fournit qu’une relation T = f (P) et, par conséquent, nécessite la connaissance indépendante de la pression de remplissage. Comme le dit E. Ingerson, la détermination de cette pression peut être très précise dans certains cas et guère mieux qu’une conjecture dans d’autres cas. En fait, certains auteurs préfèrent déterminer la température par d’autres méthodes et employer la méthode des inclusions fluides comme «manomètre».

Utilisation des états d’équilibre figés

L’hypothèse de base est la suivante: la roche était en équilibre thermodynamique à une certaine température T. À partir de cette température, le refroidissement a été suffisamment rapide pour empêcher tout réarrangement de l’édifice minéral. Par conséquent, l’étude du système figé doit fournir les paramètres physiques relatifs à l’équilibre, et en particulier la température T.

Le principal écueil est que ces paramètres sont souvent assez nombreux. La plupart des associations minérales que l’on rencontre dans les roches sont des systèmes au moins bivariants, c’est-à-dire que leur existence indique seulement un certain domaine de températures et de pressions (une certaine surface dans le plan P-T). Il existe cependant un certain nombre d’équilibres univariants, par exemple ceux qui sont liés à l’apparition ou à la disparition de certains minéraux dans le métamorphisme.

Ces réactions qui correspondent aux isogrades permettent d’établir une relation T = f (P) [une courbe dans le plan P-T]; cependant, comme la pression n’est généralement pas déterminable indépendamment, cela ne permet pas d’en déduire la température. La pente de la tangente à la courbe d’équilibre est la relation de Clapeyron:

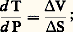sa valeur dépend des variations relatives de volume V et d’entropie S au cours de la transformation.

Deux cas limites sont intéressants pour la paléothermométrie.

Si la transformation envisagée produit un liquide ou un gaz , il y a généralement un accroissement important aussi bien du volume que de l’entropie. C’est, par exemple, le cas des réactions de déshydratation telles que:

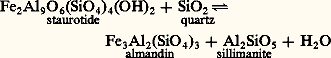ou de décarbonatation telles que:

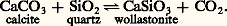Alors, pour un certain domaine de pressions «moyennes» (de 1 à 7 kbar, soit de 100 à 700 MPa), variables avec la réaction considérée, la variation d’entropie l’emporte largement sur la variation de volume, et l’on a:

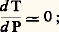c’est le cas de la plupart des treize réactions définies par Bowen dans le métamorphisme des calcaires siliceux ou par Bowen et Tuttle dans le cas des systèmes hydrosilicomagnésiens. C’est également le cas des phénomènes de fusion (par exemple, ceux qui donnent naissance aux magmas granitiques), et cela d’autant plus que la phase gazeuse (H²O, par exemple) est plus importante, car, en se mélangeant au liquide formé, elle accroît d’autant l’entropie de fusion. La figure 2 rassemble quelques-uns des équilibres pouvant servir ainsi de thermomètres géologiques. Néanmoins, leur utilisation suppose parfois la connaissance de paramètres supplémentaires qui ne sont généralement pas accessibles. On voit, par exemple, le changement introduit dans la courbe de fusion commençante du granite suivant que la pression d’eau est nulle (7 ) ou égale à la pression totale (7).

Lorsque la transformation se produit avec une variation de volume négligeable , on a encore:

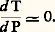Cela se produit en pratique dans deux cas importants:

– Un élément se partage entre deux phases solides. La variation relative de volume est alors souvent très faible et, comme les volumes molaires des solides sont eux-mêmes faibles, on aboutit à un V négligeable par rapport à S. Cela est particulièrement intéressant quand l’élément en question est un élément en traces qui ne conditionne pas l’existence ou la disparition d’une phase (cf. éléments en TRACES). Alors, les bilans de matière sont très simples à écrire et l’équilibre de partage se traduit très facilement.

– Les propriétés du soluté sont suffisamment voisines de celles du solvant pour que la solution soit quasi idéale quelle que soit la concentration. C’est typiquement le cas des mélanges d’isotopes des éléments ^{[cf. ISOTOPES]}, qui, de plus, peuvent généralement être considérés aussi comme le partage d’un élément en traces, car l’un des isotopes est le plus souvent nettement prépondérant (¹⁸O et D représentent respectivement des concentrations-traces dans ¹⁶O et H, isotopes prépondérants).

Avec ces deux exemples, nous entrons réellement dans le domaine de la thermométrie.

Thermomètres fondés sur la répartition des éléments en traces

C’est dans cette catégorie que l’on peut ranger le thermomètre imaginé par T. F. W. Barth à partir de la répartition du sodium entre la phase plagioclase et la phase feldspath alcalin ^{[cf. FELDSPATHS]}, encore que le sodium puisse difficilement être considéré comme un élément en traces; mais cela n’altère pas la portée de la méthode. Le potentiel chimique de l’élément en traces E est, à l’équilibre, le même dans les phases 1 et 2: 猪^E1 = 猪^E2; soit:

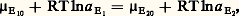où a ^E1 et a ^E2 sont les activités de E respectivement dans les phases 1 et 2 et où 猪^E10 et 猪^E20 sont ses potentiels chimiques dans les états standards correspondants (cf. THERMODYNAMIQUE – Thermodynamique chimique). Soit:

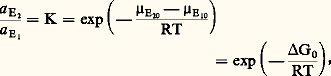où K est le coefficient de partage entre les phases 1 et 2. On peut montrer que:

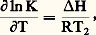où H représente la variation d’enthalpie du système au cours du passage de 1 mole de E de la phase 1 à la phase 2, et que:

Comme nous l’avons dit, V est très faible; si H ne varie pas avec la température, cela nous conduit à:

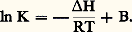Comme nous avons affaire à un élément en traces, nous pouvons appliquer les lois des solutions diluées (loi de Henry), soit:

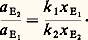Finalement nous obtenons:

où x ^E1 et x ^E2 sont les fractions molaires.

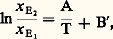Le problème est de déterminer les coefficients A et B . Cela est possible soit si l’on connaît tous les paramètres thermodynamiques du système, ce qui n’est généralement pas le cas, soit si l’on peut mesurer expérimentalement la variation de K avec la température. Dans le cas du thermomètre de Barth, la relation K = f (T) a été établie d’après des estimations indépendantes de la température de formation d’un certain nombre de roches. Un travail analogue a été fait en déterminant la répartition d’un vrai élément en traces, le nickel (en concentrations de 50 à 1 500 p.p.m.), entre les minéraux et le verre dans les laves du Makaopuhi à Hawaii, expériences au cours desquelles la température de la lave a été déterminée directement avant refroidissement rapide. Les résultats obtenus, exposés dans la figure 3, montrent que ln K varie effectivement linéairement avec 1/T. On dispose donc d’un thermomètre relativement précis et sensible pour les hautes températures, car K d’olivine-pyroxène, par exemple, varie assez rapidement avec T. Un thermomètre du même genre utilise la répartition du titane et du fer dans les phases magnétite (cubique) et ilménite (rhomboédrique). Ce système possède l’avantage de se trouver dans un assez grand nombre de roches et d’être, par conséquent, un géothermomètre assez général. En revanche, son comportement est plus compliqué, car le fer et le titane ne sont pas des éléments en traces dans les phases considérées. De plus, les passages d’une phase à l’autre impliquent également des réactions d’oxydoréduction. soit:

(constante d’équation K¹), et: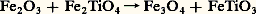

(constante d’équation K²); il leur correspond une variable supplémentaire qui est la fugacité de l’oxygène f ^O2, mais l’expression des constantes K¹ et K² permet d’éliminer f ^O2, en supposant que K¹ et K² ne dépendent pas de la pression totale, ce qui est vérifié dans la limite de précision des mesures. A. F. Buddington et D. H. Lindsley ont ainsi déterminé dans le plan f ^O2-T les courbes représentant la composition des phases magnétite et ilménite en équilibre (fig. 4). Le point d’intersection des deux courbes magnétite (Mt, Usp) et ilménite (Hém, Ilm) correspondant à une roche déterminée fournit la fugacité de l’oxygène et la température.

Les thermomètres isotopiques

En fait, le géothermomètre universel est normalement celui qui est fondé sur les fractionnements isotopiques d’un élément léger entre deux espèces chimiques ou minérales. Si l’on considère, par exemple, la silice et l’eau, les isotopes de l’oxygène s’y échangent suivant la réaction:

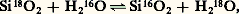et la répartition atteint un équilibre défini par le coefficient de fractionnement:

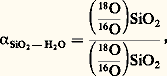Comme le remplacement d’un atome par son isotope ne s’accompagne d’aucune variation de volume, 見 est fonction uniquement de la température, indépendamment de tout autre paramètre (pression partielle de tel ou tel gaz, etc.). On a donc affaire à un vrai géothermomètre. Par ailleurs, il est universel. En effet, l’oxygène est présent dans l’immense majorité des minéraux. D’autre part, pour les minéraux non oxygénés, on dispose d’autres éléments: carbone (¹³C¹²C), soufre (³⁴S³²S) ou même hydrogène (D/H). Il suffit par conséquent de déterminer la variation de 見 avec la température. Cette relation peut être trouvée soit expérimentalement, soit par le calcul en utilisant les données spectroscopiques et les méthodes de calcul de la thermodynamique statistique. C’est ainsi qu’ont été déterminés expérimentalement pour l’oxygène les coefficients de fractionnement entre eau et quartz, eau et feldspaths (orthose, albite, anorthite), eau et muscovite

et paragonite, eau et calcite. Un certain nombre de coefficients 見 ont été calculés pour l’oxygène entre l’eau, le gaz carbonique et la calcite, pour le carbone et l’hydrogène dans le système eau-gaz carbonique-méthane-hydrogène-carbone (graphite et diamant).

Les compositions isotopiques se rapportent généralement en variation du rapport isotopique en pour mille par rapport à celui d’un standard (eau de mer moyenne pour l’oxygène et l’hydrogène, PDB pour le carbone, etc.); soit, par exemple,

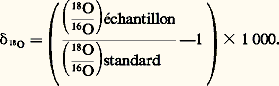Comme les 嗀 ne varient généralement que de quelques dizaines au plus, on peut écrire:

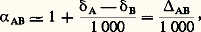où ^AB est le fractionnement entre A et B. On a évidemment:

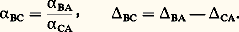Le fractionnement tend vers zéro quand T augmente indéfiniment ( 見1, 0). Dans le domaine des très hautes températures (T 閭 1 000 ⁰C), 1 000 ln 見 = = a ². Pour les températures moins élevées, les expressions dépendent des couples considérés, mais se met très généralement sous la forme d’un polynôme en 1/T; couramment, = a + b ² ou = a + b /T, ces formules n’étant valables que dans un intervalle défini de températures. Dans le domaine des basses températures (de 0 à 50 ⁰C, par exemple), on extrait souvent T de ces expressions sous la forme d’un développement en puissances de , avec T exprimé en degrés Celsius:

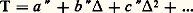La géochimie isotopique a été lancée par Harold C. Urey vers 1947, et l’un des éléments les plus spectaculaires de ce lancement a été justement la détermination des températures sous lesquelles vivaient un certain nombre d’espèces fossiles telles que les bélemnites. En mesurant la composition isotopique de la calcite de ces fossiles et en supposant que la composition isotopique de l’eau de mer n’ait pas varié depuis l’ère secondaire, Urey et ses collaborateurs, puis Cesare Emiliani et d’autres obtinrent des courbes d’évolution des températures moyennes au cours des époques géologiques avec différents cycles, ainsi que les variations ayant affecté un individu donné par l’étude de ses zones de croissance successives.

L’emploi du thermomètre isotopique s’est ensuite généralisé à tous les types de roches (et à des fossiles non calcaires comme les diatomées, à squelettes siliceux), une fois qu’eurent été résolus les problèmes difficiles d’extraction (oxygène des silicates, en particulier). La mesure des fractionnements entre minéraux dans les principaux types de roches métamorphiques, les granites, les roches basiques plutoniques et un certain nombre de roches volcaniques a permis de déterminer des «températures isotopiques». L’utilisation de plusieurs couples de minéraux permet de vérifier l’hypothèse de l’équilibre thermodynamique par l’égalité des températures obtenues. Ces mesures, effectuées depuis 1960 environ par différentes équipes, représentent les seules déterminations directes de paléotempératures faites indépendamment de toute hypothèse restrictive sur les conditions de pression ou d’environnement chimique. Pour les principales catégories de roches, elles tombent dans les limites qu’on avait précédemment supposées. Le tableau indique ces températures comparées à celles du thermomètre ilménite-magnétite. Cependant, on remarque généralement que les températures obtenues pour les roches volcaniques correspondent très sensiblement à la température de solidification de la lave, alors que, pour les roches plutoniques, elles sont généralement plus basses que les températures de cristallisation qu’on peut estimer d’après les synthèses de laboratoire. Cela signifie que les échanges isotopiques ont continué pendant le refroidissement lent de ces roches, ce qui est vrai également pour un certain nombre de roches métamorphiques. On peut donc en conclure – et cela vaut également pour d’autres thermomètres tels que le thermomètre ilménite-magnétite – que, dans ce cas, les «températures» obtenues représentent celles à partir desquelles les vitesses de réaction et d’échange sont devenues trop faibles par rapport à la vitesse de refroidissement pour assurer le maintien de l’équilibre thermodynamique. Les indications qu’elles donnent peuvent néanmoins être précieuses pour fixer justement la vitesse de ce refroidissement (et, à partir de là, la température de l’encaissant dans lequel a eu lieu la cristallisation d’un magma), la vitesse de remontée d’un matériel métamorphique après la culmination du métamorphisme, etc. Cela ouvre un champ encore à peine exploré à cause des études préalables de cinétique d’échange qu’il suppose.

Encyclopédie Universelle. 2012.